图数据挖掘：社区检测算法（一）
最近需要学习图结构中的社区检测算法，在阅读相关论文的同时跟了Stanford CS246课程的第11讲Community Detection in Graphs，本篇博客我做的笔记。我们通常认为网络中存在某种模块(modules)/簇(clusters)/社区(communitis)结构，我们常常需要从网络中提取这些结构。而提取这些结构的关键在于发现密集连接的簇，而这常常可以转化为一个优化关于簇的目标函数的问题。按照图的社区划分之间是否重叠，可分为重叠社区检测和非重叠社区检测。非重叠社区检测是指图的社区划分之间没有重叠，而重叠社区检测则允许有重叠。
最近需要学习图结构中的社区检测算法，在阅读相关论文的同时跟了Stanford CS246: Mining Massive Datasets课程[1]的第11讲Community Detection in Graphs，以下是我做的笔记。
1. 网络和社区(networks & communities)
我们通常认为网络中存在某种模块(modules)/簇(clusters)/社区(communitis)结构，我们常常需要从网络中提取这些结构。
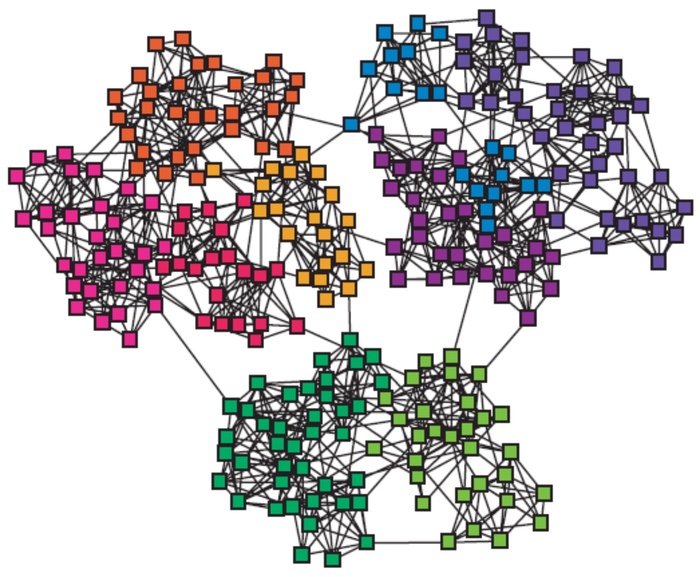
而提取这些结构的关键在于发现密集连接的簇，而这常常可以转化为一个优化关于簇的目标函数的问题。
2.重叠(overlapping)和非重叠(non-overlapping)社区检测
按照图的社区划分之间是否重叠，可分为重叠社区检测和非重叠社区检测。非重叠社区检测是指图的社区划分之间没有重叠，而重叠社区检测则允许有重叠。
3.基于conductance（电导）的图划分方法
3.1 割分数(cut score)
设有一个无向图\(G(V,E)\)，我们将其节点划分为两个组\(A, B\)，其中\(B = V\backslash A\)，我们如何判断我们划分的质量呢？
我们运用直觉思考，好的划分有什么特性？一般而言，好的划分有两个特点：
- 使单个簇内部的连接数量最大化
- 使不同簇之间的连接最小化
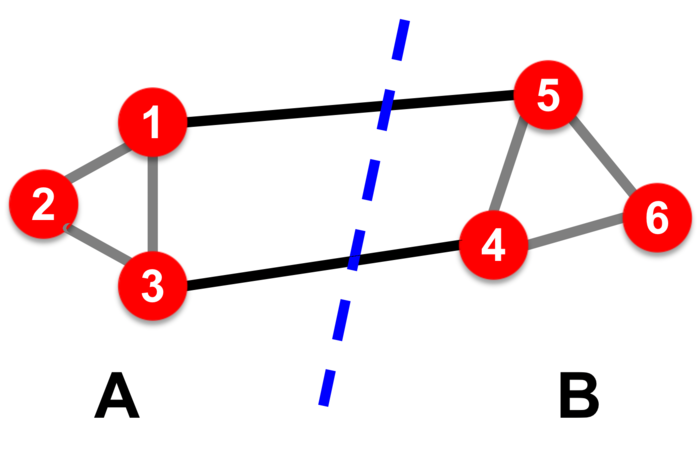
接下来我们需要定量地将簇的质量表示为该簇的“edge cut”（感觉翻译成割边不太妥当，为了表述方便，下面将两个簇之间连接的边形象地称为“跨边”）的函数。
割分数(cut score) 为只有一个节点在簇中的边的边权之和（如果为无权图，则权值计为1）。用公式表达如下：
对于下面这张无权图，则我们有\(cut(A) = 2\):
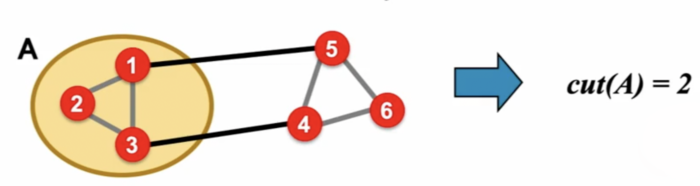
也就是说，对于一个簇\(A\)，若\(cut(A)\)越小，则我们说这个簇的质量越好。那么所谓的簇划分，是否意味着我们只需要找到一组能够时\(cut(A)\)尽量小的节点就可以呢？
光这样还不够，因为我们事实上只考虑了簇外部的联系，但是没有考虑簇内部的联系，这样容易导致很多问题。我们看下面这个退化的情形。很明显，就下面这张图而言，红色的所谓“mimimum cut”确实做到使\(cut(A)\)最小了，但是明显另外一种划分方法才是我们想要的。
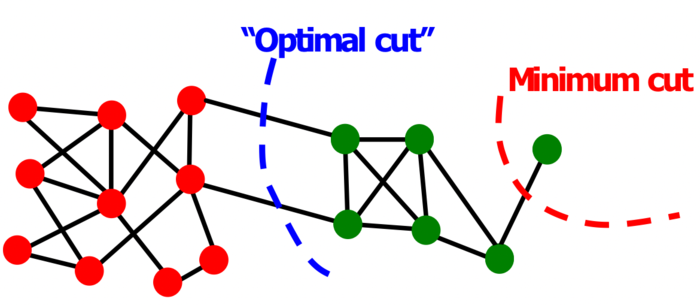
那么我们如何进一步考虑到簇内部的联系呢？这时就要引出簇的volume(体积)和conductance（好像翻译成电导？）的概念了。
3.2 电导(conductance)
conductance是指一个簇和剩余网络的联系，它和这个簇的的密度（体积）有关系。它在某种意义上可以理解为表面积和体积比(surface-to-volume ratio)。直观地理解，它等于这个簇的割分数除以这个簇自身的密度（体积），这个值越小说明划分得越好。
接下来我们再来看conductance这个有点可怕的公式（其实理解了它的意义后就会发现并不可怕）：
此公式中\(m\)指图中边的数量，\(2m\)即图中所有点的度数之和，\(E\)指图的边集。\(vol(A)\)定义为簇\(A\)中所有点的度之和：
\[\begin{aligned} vol(A) &= \sum_{i\in A} d_{i} \end{aligned}\\ (这里d_i指节点i的度) \](也可以写作\(vol(A)= 2\cdot \sharp\text{edges inside } A + \sharp \text{edges pointing out of } A\))
\(\phi(A)\)定义式的分母部分实质上就相当于从割边分开的两个簇的\(vol\)值中选小的那个。
我们再来用conductance重新审视图的划分。
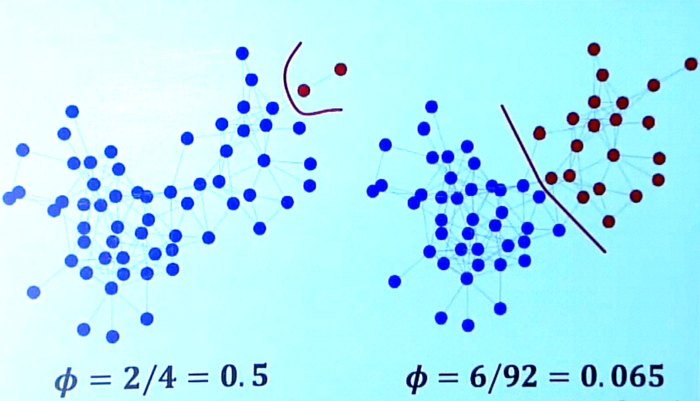
很明显，若我们关注红色的簇，边的那种划分方式\(\phi = 2/(3+1)=0.5\)(其中\(2\)为红色簇跨出去的边数之和，\(3+1=4\)为红色簇的度数之和)，右边的那种划分方式\(\phi = 6/92=域名\)，很明显右边的那种划分方式更好。
根据这个划分标准，有许多论文已经提出了相关的簇划分算法，如[2]，大家可以参考论文，此处略过不表。
4.基于模块性(modularity)的图划分方法
4.1 模块性
对于一个网络社区，我们定义其模块性(modularity)\(Q\)做为一个网络被划分为社区的好坏度量。给定一个网络的划分，该划分将网络划分为由多个组\(s\)组成的集合\(S\)，我们有:
\[Q \varpropto \sum_{s\in S}[(\sharp \text{edges within group }s) - (\text{expected }\sharp \text{edges within group } s)] \]我们给定一个有\(n\)个节点和\(m\)条边的图，我们据此构建重布线的(rewired)网络\(G^{\'}\)。该网络\(G^{\'}\)满足：有同样的度分布但是有着随机的边连接；是多重图(multigraph)（即允许有多重边的图）；节点\(i\)（度为\(k_i\)）和\(j\)(度为\(k_j\))之间的期望边数量为：\(k_i \cdot \frac{k_j}{2m} = \frac{k_i k_j}{2m}\)。
我们根据以上信息，进一步图\(G\)被划分为组\(S\)的模块性写为
这里\(m\)为一个标准化常数，使得\(-1<Q<1\)。\(A_{ij}\)为节点\(i\)和节点\(j\)之间的边权，若无连接则为0。
如果在簇内部的边数量超过了其期望的边数量，则模块性\(Q\)为正。比\(0.3-0.7\)大的\(Q\)意味着非常重要的社区结构。
等效地，模块性公式还能够被写作：
\[Q=\frac{1}{2 m} \sum_{i j}\left[A_{i j}-\frac{k_{i} k_{j}}{2 m}\right] \delta\left(c_{i}, c_{j}\right) \]这里\(A_{ij}\)仍然指节点\(i\)和\(j\)之间的边权，\(k_i\)分别\(k_j\)指以节点\(i\)和\(j\)做为端点的边权之和，\(2m\)是凸中所有边的权值之和，\(c_i\)和\(c_j\)是节点组成的社区，\(\delta\)是一个示性函数。此时，我们有一个想法： 我们能够通过最大化模块性\(Q\)来识别社区。
4.2 Louvain（鲁汶）方法
我们可以采用一个启发式方法，也就是Louvain方法来解决该问题。这个算法是一个贪心算法，时间复杂度为\(O(n log n)\)，它支持带权图，能够提供层次化的划分方法（比如我们熟知的层次聚类）。该方法运行效率高、收敛快、输出结果模块性高（也即输出的社区划分质量较好），被广泛地应用于大规模网络。
Louvain算法贪心地最大化模块性，它会进行多轮的迭代，每一轮迭代都由两个步骤组成：
- 步骤 1（划分）：在只允许对社区做局部改变(local changes)的情况下优化模块性，得到一个初步的社区划分。
- 步骤 2（重构）：对已划分出的社区做聚合，建立新的社区网络。
我们接下来详细地叙述步骤1和步骤2。
步骤1（划分）
对于步骤1，算法先将图中的每个节点(后面我们会提到算法会将社区也缩为一个超节点)视为一个独立的社区。然后对每个节点\(i\)，算法执行两步计算：首先，对节点\(i\)的每个邻居\(j\)，计算将\(i\)从其现在的社区中放入\(j\)所在的社区时可获得的模块性增益(modularity gain)\(\Delta Q\)；然后，将\(i\)移入能够获得最大\(\Delta Q\)的社区。
注：
当我们将节点\(i\)移入社区\(C\)中时，其模块性增益\(\Delta Q\)计算方式如下：
\[\Delta Q(i \rightarrow C)=\left[\frac{\sum_{i n}+k_{i, i n}}{2 m}-\left(\frac{\sum_{t o t}+k_{i}}{2 m}\right)^{2}\right]-\left[\frac{\sum_{i n}}{2 m}-\left(\frac{\sum_{t o t}}{2 m}\right)^{2}-\left(\frac{k_{i}}{2 m}\right)^{2}\right] \]这里\(\sum_{in}\)对\(C\)中所有节点的"簇内"邻边（不包括跨边）的边权进行求和；\(\sum_{tot}\)对\(C\)中所有节点的邻边（包括跨边）边权进行求和;\(k_{i, in}\)是节点\(i\)和簇\(C\)之间的所有边的权重之和；\(k_i\)指节点\(i\)所有邻边的权重之和（其实就是节点的度，注意带权图节点的度定义为节点所有邻边的权值和）。
同理，我们可以得到\(\Delta Q(D\rightarrow i)\)，这表示将节点\(i\)移出社区\(D\)所得的增益。
接下来，我们有\(\Delta Q=\Delta Q(i \rightarrow C)+\Delta Q\left(D\rightarrow i\right)\)
步骤2（重构）
将第一阶段中划分而成的社区缩为超节点(super-nodes)，然后我们按照以下的步骤来构建新的带权网络：如果在两个社区的节点之间至少有一条边，那么对应的两个超节点之间就是连接的；在两个超节点之间的边的权值是其对应社区之间所有跨边的权值之和。
最后，我们将Louvain方法用流程示意图描述如下：
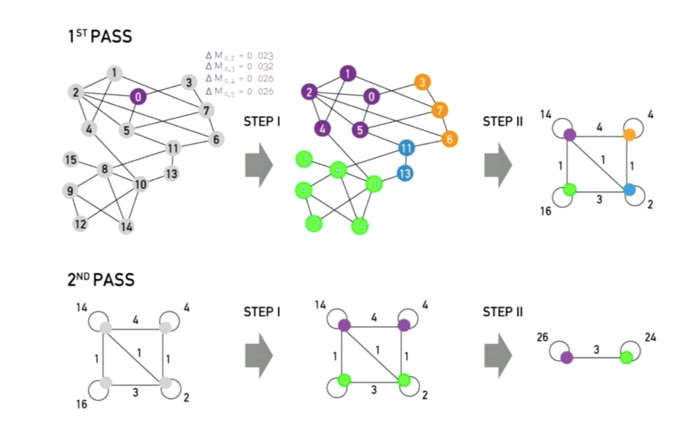
参考文献
- [1] http://域名/
- [2] Lu Z, Sun X, Wen Y, et al. Algorithms and applications for community detection in weighted networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2014, 26(11): 2916-2926.
- [3] Staudt C L, Meyerhenke H. Engineering parallel algorithms for community detection in massive networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2015, 27(1): 171-184.
